Brief Instructions:
Figure of Mandelbrot
set M
({Z∈M
| Cn+1 = Cn2
+ Z, |Cn|
is bounded when n→ ∞})
is shown.
Analysis of the figure can be done by using the zoom functions
and changing the parameters.
- Zoom functions:
- Click and drag
the figure to zoom arbitrary rectangle area on the figure.
- Click "Redraw"
button to redraw the figure.
- Click "Undo"
button to undo the previous operation.
- Click "X2"
button to zoom the figure.
- Click "/2"
button to zoom out the figure.
- Click "Color
Table" button or "Hue Coloration"
button to change coloration method.
- Click "Reset"
button to initialize.
- Parameters:
- Set "Julia
Re" to change the ℜC0.
- Set "Julia
Im" to change the ℑC0.
- Set "Threshold"
to change the threshold for the magnitude of the final
C:
C∞2.
- Set "Iteration"
to change the maximum number of the iteration.
- Click "Apply"
button to apply the changes of the parameters.
- Click "Initialize"
button to initialize the parameters.

ℜ
= [-0.16, -0.16], ℑ
= [1.026, 1.028] (Color
Table)
|
|
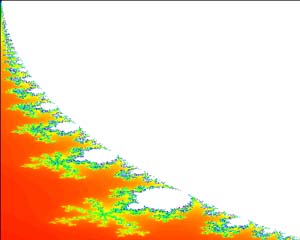
ℜ
= [-0.75, -0.51], ℑ
= [0.023, 0.509] (Hue
Coloration)
|
| |
|
|

ℜ
= [-0.87, -0.64], ℑ
= [-0.35, -0.01] (Color
Table) |

ℜ
= [-0.22, -014], ℑ
= [1.012, 1.124] (Hue
Coloration) |
| |
|

ℜ
= [-0.41, -0.32], ℑ
= [-0.68, -0.59] (Color
Table)
|

ℜ
= [-0.41, -0.32], ℑ
= [-0.68, -0.59] (Hue
Coloration)
|
The Mandelbrot set, named
after Benoit Mandelbrot, is a fractal. Fractals are objects
that display self-similarity at various scales. Magnifying a fractal
reveals small-scale details similar to the large-scale characteristics.
Although the Mandelbrot set is self-similar at magnified scales,
the small scale details are not identical to the whole. In
fact, the Mandelbrot set is infinitely complex. Yet the process
of generating it is based on an extremely simple equation involving
complex numbers.
The Mandelbrot set is
a set of complex numbers, so we graph it on the complex number plane.
However, first we have to find many numbers that are part of the
set. To do this we need a test that will determine if a given number
is inside the set or outside the set. The test is based on the equation:
Cn+1 = Cn2 + Z.
Z
represents a constant number, meaning that it does not change
during the testing process. Z
is the number we are testing, the point on the complex plane that
will be plotted when testing is complete. C
starts out as C0
= a + bi, and we call a
and b as "Julia Re" and "Julia Im",
respectively. But C
changes as we repeatedly iterate this equation. With each
iteration we create a new C
that is equal to the old C
squared plus the constant Z.
So the number C
keeps changing throughout the test.
mandelbrotSet.java
 (Comments are in Japanese (Comments are in Japanese  .) .)
Further reading:
D. Dewey, "Introduction
to the Mandelbrot Set", The Web, http://www.ddewey.net/mandelbrot/ ,
(2002). ,
(2002).
|
Applet | 
Supplementary Information: Ryoichi Mizuno - Google+  
|