Mandelbrot Set

Brief Instructions:

| This applet | Control | Examples | Mandelbrot set | Source code |

This applet:

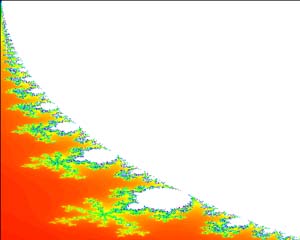
Figure of Mandelbrot set M ({Z∈M | C_n+1 = C_n² + Z, |C_n| is bounded when n→ ∞}) is shown.
Analysis of the figure can be done by using the zoom functions and changing the parameters.

Control:

• Zoom functions:
  • Click and drag the figure to zoom arbitrary rectangle area on the figure.
  • Click "Redraw" button to redraw the figure.
  • Click "Undo" button to undo the previous operation.
  • Click "X2" button to zoom the figure.
  • Click "/2" button to zoom out the figure.
  • Click "Color Table" button or "Hue Coloration" button to change coloration method.
  • Click "Reset" button to initialize.

• Parameters:
• Set "Julia Re" to change the ℜC₀.
• Set "Julia Im" to change the ℑC₀.
• Set "Threshold" to change the threshold for the magnitude of the final C: C_∞².
• Set "Iteration" to change the maximum number of the iteration.
• Click "Apply" button to apply the changes of the parameters.
• Click "Initialize" button to initialize the parameters.

Examples:

ℜ = [-0.16, -0.16], ℑ = [1.026, 1.028] (Color Table)		ℜ = [-0.75, -0.51], ℑ = [0.023, 0.509] (Hue Coloration)
ℜ = [-0.87, -0.64], ℑ = [-0.35, -0.01] (Color Table)		ℜ = [-0.22, -014], ℑ = [1.012, 1.124] (Hue Coloration)
ℜ = [-0.41, -0.32], ℑ = [-0.68, -0.59] (Color Table)		ℜ = [-0.41, -0.32], ℑ = [-0.68, -0.59] (Hue Coloration)

Mandelbrot set:

The Mandelbrot set, named after Benoit Mandelbrot, is a fractal. Fractals are objects that display self-similarity at various scales. Magnifying a fractal reveals small-scale details similar to the large-scale characteristics. Although the Mandelbrot set is self-similar at magnified scales, the small scale details are not identical to the whole. In fact, the Mandelbrot set is infinitely complex. Yet the process of generating it is based on an extremely simple equation involving complex numbers.

The Mandelbrot set is a set of complex numbers, so we graph it on the complex number plane. However, first we have to find many numbers that are part of the set. To do this we need a test that will determine if a given number is inside the set or outside the set. The test is based on the equation:

C_n+1 = C_n² + Z.

Z represents a constant number, meaning that it does not change during the testing process. Z is the number we are testing, the point on the complex plane that will be plotted when testing is complete. C starts out as C₀ = a + bi, and we call a and b as "Julia Re" and "Julia Im", respectively. But C changes as we repeatedly iterate this equation. With each iteration we create a new C that is equal to the old C squared plus the constant Z. So the number C keeps changing throughout the test.

Source code:

mandelbrotSet.java (Comments are in Japanese .)

Further reading:
D. Dewey, "Introduction to the Mandelbrot Set", The Web, http://www.ddewey.net/mandelbrot/, (2002).

| Page top |
Supplementary Information: Ryoichi Mizuno - Google+