 | English | | English |

ローレンツアトラクタ
— ローレンツアトラクタを描画する,
あるいはそれに類似することをするときのために. —

ソースコード
l1.c
/* ローレンツ方程式のカオスのストレンジアトラクタを描く. */
/*
** ローレンツ方程式の説明についてはlorenz.hのコメント文を参照せよ.
** アトラクタとは時間とともに体積が縮小する散逸力学系において
** 過渡状態経過後の定常状態のことである.
** カオスのアトラクタを特に, ストレンジアトラクタト呼ぶ.
** 常微分方程式の数値計算にはルンゲクッタ法を用いた.
** ルンゲクッタ法の説明についてはrk.hのコメント文を参照せよ.
** 描画にはgnuplotを用いた.
** このプログラムはlinuxで動作確認している.
*/
#include <stdio.h>
#include <stdlib.h>
#include "rk.h"
#include "lorenz.h"
/* lorenz(double t,double X[],double dXdt[]) */
#define N 3 /* 状態変数の次元 */
#define h 0.01 /* ルンゲクッタステップ */
#define T 10000 /* ルンゲクッタの計算回数 */
main()
{
int t,i;
/* double X0[N],double X1[N]の配列を動的に作成 */
double *X0=vector(N),*X1=vector(N);
/* 初期値の設定 */
X0[0]=10.0;
X0[1]=20.0;
X0[2]=30.0;
/* メインパート */
for(t=0;t<=T-1;t++)
{
for(i=0;i<=N-1;i++)
{
printf("%f",X0[i]);
if(i==N-1)putchar('\n');
else putchar(' ');
}
/*
** 関数lorenzと時刻h*tのとき状態変数X0を渡し,
** 時刻h*(t+1)のとき状態変数X1を得る.
*/
rk(h,N,lorenz,h*t,X0,X1);
copy_vector(N,X1,X0);
}
return 0;
}
rk.h
/* ルンゲクッタ・ルーチン (rk.h) */
/*
** このヘッダファイルはN個の状態変数を持つ
** 1階の常微分方程式を解くためのものである.
** 3次までのルンゲクッタ法を用いる.
** コンピュータシュミレーションでは, 微分方程式
** dx(t)/dt=F(x(t),t)を解析的に求めることはできないので
** 時間tを離散化して求めることになる.
** 4次のルンゲクッタ法を式で表すと以下のようになる.
** d1=hF(x(t),t)
** d2=hF(x(t)+d1/2,t+h/2)
** d3=hF(x(t)+d2/2,t+h/2)
** d4=hF(x(t)+d3,t+h)
** x(t+h)=x(t)+d1/6+d2/3+d3/3+d4/6
** hは離散化の時間幅であるルンゲクッタステップである.
*/
#include <stdlib.h>
double *vector(int N) /* ベクトル領域の確保 */
{
/* サイズNの領域をmallocで動的に作成する */
return (double *)malloc(N*sizeof(double));
}
void free_vector(double *v) /* ベクトル領域の解放 */
{
/* ポインタvの領域を解放する */
free(v);
}
void copy_vector(int N,double a[],double b[])
/* ベクトルのコピー */
{
int i;
/* ベクトルaをベクトルbにコピーする */
for(i=0;i<=N-1;i++)b[i]=a[i];
}
/*
** ルンゲクッタステップh,微分方程式の階数N,微分方程式が記述された
** 関数dXdt,時刻tのときの状態変数が入ったベクトルX0を渡し, 時刻t+
** h の時の状態変数X1を得る. dXdtはhoge(double t,double X[],doubl
** edXdt[])の型でユーザが定義する.
*/
void rk(double h,int N,
void (*dXdt)(double t,double X[],double dXdt[]),
double t,double X0[],double X[]) /* ルンゲクッタ */
{
int i;
/* double d1[N],double d2[N],double d3[N]の配列を動的に作成 */
double *d1=vector(N),*d2=vector(N),*d3=vector(N);
/* double Xa[N]double,X[N]の配列を動的に作成 */
double *Xa=vector(N),*dX=vector(N);
/* d1=hF(x(t),t) */
dXdt(t,X0,dX);
for(i=0;i<=N-1;i++)
{
d1[i]=h*dX[i];
Xa[i]=X0[i]+0.5*d1[i];
}
/* d2=hF(x(t)+d1/2,t+h/2) */
dXdt(t+0.5*h,Xa,dX);
for(i=0;i<=N-1;i++)
{
d2[i]=h*dX[i];
Xa[i]=X0[i]+0.5*d2[i];
}
/* d3=hF(x(t)+d2/2,t+h/2) */
dXdt(t+0.5*h,Xa,dX);
for(i=0;i<=N-1;i++)
{
d3[i]=h*dX[i];
Xa[i]=X0[i]+d3[i];
}
/* x(t+h)=x(t)+d1/6+d2/3+d3/3 */
dXdt(t+h,Xa,dX);
for(i=0;i<=N-1;i++)X[i]=X0[i]
+(d1[i]+d2[i]*2+d3[i]*2+h*dX[i])/6.0;
/* 各配列の領域の解放 */
free_vector(d1);free_vector(d2);free_vector(d3);
free_vector(Xa);free_vector(dX);
}
lorenz.h
/* ローレンツ方程式 (lorenz.h) */
/*
** このヘッダファイルはローレンツ方程式の関数の型を
** ルンゲクッタ・ルーチン (rk.h)のために記述する.
** ローレンツ方程式とは, 大気の対流現象の大幅な近似の下でのモデルで,
** 3変数の常微分方程式である.
** dx/dt=-σx+σy
** dy/dt=-xz+rx-y
** dz/dt=xy-bz
** σ,b,rはパラメータであり, ここでは
** σ=10,b=8/3,r=28とする.
** ローレンツ方程式は初期値に対して鋭敏に反応する
** これは, バタフライ効果の語源になった現象である.
*/
/* 関数および変数の表記をrk.hと整合させる */
#define dxdt dXdt[0]
#define dydt dXdt[1]
#define dzdt dXdt[2]
#define x X[0]
#define y X[1]
#define z X[2]
/* ローレンツ方程式 */
void lorenz(double t,double X[],double dXdt[])
{
double sigma=10.0,b=8.0/3,r=28.0;
dxdt=-sigma*x+sigma*y;
dydt=-x*z+r*x-y;
dzdt=x*y-b*z;
}
/* 定義の解除 */
#undef dxdt
#undef dydt
#undef dzdt
#undef x
#undef y
#undef z
|
結果
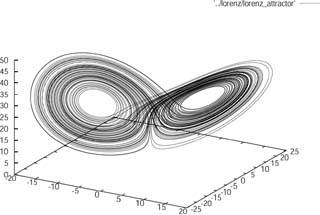
Fig. 1: ローレンツアトラクタ
(PS, PDF, PSD, PSD (for the web), AI).
付録
gnuplot
を用いて, シダ植物を描画した例を Fig. 2 に示す.
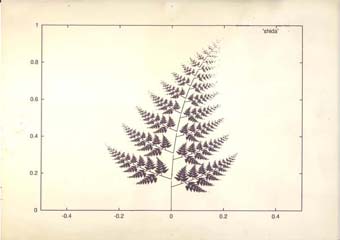
Fig. 2: シダ植物.
| Top page |
Feedback
Message Form  
Supplementary Information: Ryoichi Mizuno - Google+  
Created: 2005/05/10
Copyright © 2001-2014 Ryoichi Mizuno, All Rights Reserved.
|
![]() | English |
| English |
![]()

![]()
![]()

