|
|
The Lorenz Attractor
— For drawing the Lorenz attractor,
or coping with a similar situation. —
Source code
/* Drawing the strange attractor of chaos of the Lorenz equations. */
/*
** For explanation of the Lorenz equations refer to the comments of 'lorenz.h'.
** An attractor is the stationary state after a long enough time in dissipative ** dynamical system.
** That volume reduces with respect to time passage.
** Especially, the attractor of chaos is called as the strange attractor. ** The Runge-Kutta method was used for the numerical calculation of the ** ordinary differential equations. ** Refer to the comments of 'rk.h' for the Runge-Kutta method.
** For drawing "gnuplot" was used.
** The checking of operations of these programs had been done several ** versions of Linux. */ #include <stdio.h> #include <stdlib.h> #include "rk.h" #include "lorenz.h" /* lorenz(double t, double X[], double dXdt[]) */ #define N 3 /* dimension of state variable */ #define h 0.01 /* Runge-Kutta step */ #define T 10000 /* Numbers of caculation of Runge-Kutta */ main() { int t, i; /* Dynamically allocating arrays for 'double X0[N],' and 'double X1[N]'. */ double *X0 = vector(N),*X1 = vector(N); /* Initial setting */ X0[0] = 10.0; X0[1] = 20.0; X0[2] = 30.0; /* Main part */ for(t = 0; t < = T - 1; t++) { for(i = 0; i < = N - 1; i++) { printf("%f", X0[i]); if(i == N - 1) putchar('\n'); else putchar(' '); } /* ** Putting the function 'lorenz' and the state variable 'X0' at time ** 'h*t' to get the state variable 'X1' at time 'h*(t+1)'. */ rk(h,N, lorenz, h*t, X0, X1); copy_vector(N, X1, X0); } return 0; }
/* Runge-Kutta routine (rk.h) */ /* ** This header file is for resolving a rank-1 ordinary differential equations. ** The number of state variables of each equation is 'N'. ** This time, the Runge-Kutta method was used. The order is up to 3. ** Since using computer simulation cannot resolve analytically ** the differential equation 'dx(t) / dt = F(x(t), t),' ** the time 't' should be discretized. ** The order 4 Runge-Kutta method is as follows: ** d1 = hF(x(t), t), ** d2 = hF(x(t) + d1 / 2, t + h / 2), ** d3 = hF(x(t) + d2 / 2, t + h / 2), ** d4 = hF(x(t) + d3, t + h), ** x(t + h) = x(t) + d1 / 6 + d2 / 3 + d3 / 3 + d4 / 6, ** , where 'h' is the size of discretized time, and is the Runge-Kutta step. */ #include <stdlib.h> double *vector(int N) /* Allocating vector region */ { /* ** Dynamically allocating an array using "malloc". ** The size of the array is 'N'. */ return (double *)malloc(N * sizeof(double)); } void free_vector(double *v) /* Releasing vector region */ { /* Releasing the region of the pointer 'v'. */ free(v); } void copy_vector(int N, double a[], double b[]) /* Copying vectors */ { int i; /* Copying the vector 'a' to the vector 'b' */ for(i = 0; i <= N - 1; i++) b[i] = a[i]; } /* ** Putting the Runge-Kutta step 'h,' the rank of the differential equation N, ** the function 'dXdt' which describes the differential equation, ** and the vector 'X0' which contains the state variable at time 't' ** to get the state variable 'X1' at time 't + h'. ** 'dXdt,' which type is 'foo(double t, double X[], double dXdt[])' should be ** defined by user. */ void rk(double h, int N, void (*dXdt)(double t, double X[], double dXdt[]), double t, double X0[], double X[]) /* Runge-Kutta */ { int i; /* ** Dynamically allocating arrays for 'double d1[N],' 'double d2[N],' ** and 'double d3[N]'. */ double *d1 = vector(N),*d2 = vector(N),*d3 = vector(N); /* ** Dynamically allocating arrays for 'double Xa[N],' and 'double X[N]'. */ double *Xa = vector(N),*dX = vector(N); /* d1 = hF(x(t), t) */ dXdt(t, X0, dX); for(i = 0; i <= N - 1; i++) { d1[i] = h * dX[i]; Xa[i] = X0[i] + 0.5 * d1[i]; } /* d2 = hF(x(t) + d1 / 2, t + h / 2) */ dXdt(t + 0. 5 * h, Xa, dX); for(i = 0; i <= N - 1; i++) { d2[i] = h * dX[i]; Xa[i] = X0[i] + 0.5 * d2[i]; } /* d3 = hF(x(t) + d2 / 2, t + h / 2) */ dXdt(t + 0.5 * h, Xa, dX); for(i = 0; i <= N-1; i++) { d3[i] = h * dX[i]; Xa[i] = X0[i] + d3[i]; } /* x(t + h) = x(t) + d1 / 6 + d2 / 3 + d3 / 3 */ dXdt(t + h, Xa, dX); for(i = 0; i <= N - 1; i++) X[i] = X0[i] + (d1[i] + d2[i] * 2 + d3[i] * 2 + h * dX[i]) / 6.0; /* Releasing the regions of arrays */ free_vector(d1); free_vector(d2); free_vector(d3); free_vector(Xa); free_vector(dX); }
lorenz.h
/* The Lorenz equations (lorenz.h) */ /* ** This header file describes function type of the Lorenz equations ** for the Runge-Kutta routine (rk.h). ** The Lorenz equations derived by simplifying of convection rolls arising ** in the atmosphere, and described as ordinary differential equations ** that have 3 variables: ** dx / dt = -δx + δy, ** dy / dt = -xz + rx - y, ** dz / dt = xy - bz, ** , where δ, b, and r are parameters, and this time, they are set to ** as follows: ** δ = 10, b = 8 / 3, and r = 28. ** The Lorenz equations exhibit sensitive dependence on initial conditions.
** This phenomenon is used as the root of "the butterfly effect". */ /* The notation of functions and variables are consistent with 'rk.h'. */ #define dxdt dXdt[0] #define dydt dXdt[1] #define dzdt dXdt[2] #define x X[0] #define y X[1] #define z X[2] /* The Lorenz equations */ void lorenz(double t, double X[], double dXdt[]) { double sigma=10.0, b=8.0 / 3, r=28.0; dxdt = -sigma * x + sigma * y; dydt = -x * z + r * x - y; dzdt = x * y - b * z; } /* releasing the definitions */ #undef dxdt #undef dydt #undef dzdt #undef x #undef y #undef z
Result
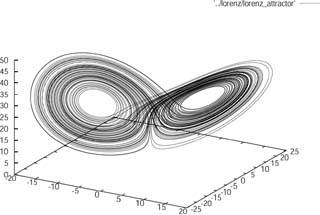
Fig. 1: The Lorenz Attractor
(PS, PDF,
PSD, PSD
(for the web), AI).
Appendix
Fig. 2 demonstrates a pteridophyte (fern) drawn by using "gnuplot![]() ":
":
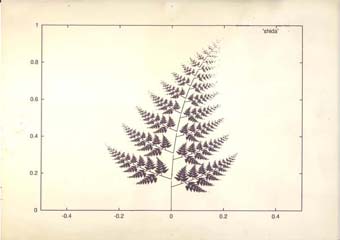
Fig. 2: A pteridophyte (fern).
| Top page |
Feedback
![]()
Supplementary Information: Ryoichi Mizuno - Google+ ![]()
![]()
Created: 2008/05/14
Copyright © 2001-2008 Ryoichi Mizuno, All Rights Reserved.
