![]() |
| ![]() |
| ![]()
![]() Tweet
Tweet
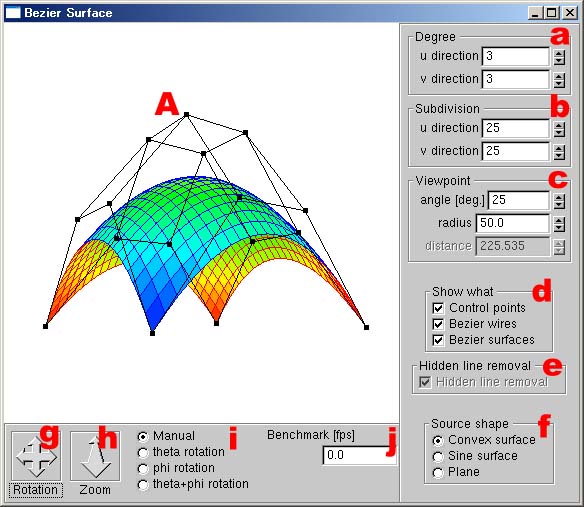
Bézier Surface
|
|
DOWNLOAD DOWNLOAD SOURCE CODE
MOVIE MOV (5.32MB) (QuickTime |
Index
1 Overview
2 Development Environment
3 Requirements
4 Specification
(Moving Control Point, Changing Degree, Changing Number of Division, Changing Visual Distance, Show/Hide Objects, Enable/Disable Hidden Surface/Line Removal, Original Shape, Rotation of Viewpoint, Zoom In/Out, Manual/Automatic Animation, and Benchmark Test)
5 Reported Bug/Disorder
1 Overview
- A degree n×m Bézier surface can be drawn.
- The degree and the number of division can be set arbitrary.
- The control points can be moved intuitively.
- The perspective projection and the hidden surface/line removal are implemented intentionally not to use any hardware resource such as GPU.
- Some shapes cannot be drawn correctly due to the usage of the Z-sorting.
|
Fig. 1: A captured image of the application (running on Windows XP Professional). |
| Top |
2 Development Environment
- C++ (ANSI)
- OpenGL (GLUT for Win32 version 3.7.3, GLUI for Win32 version 2.0 beta)
| Top |
3 Requirements
3.1 Binary
- bs.exe (binary / 188KB)
→ Windows 95 SR2/98/98 SE/ME/NT4.x/2000/XP/2003
glut32.dll (DLL / 160KB) is required.
3.2 Source Code
- HTML version
 (the comments are in Japanese, and will be not translated; to read use translator, e.g. Google's Language Tools
(the comments are in Japanese, and will be not translated; to read use translator, e.g. Google's Language Tools .)
.)
→ UNIX (X Window System), Windows 95/98/ME/NT/2000/XP, OS/2, Mac OS, Be OS, etc.
For X Window System, including glx.h is required.
| Top |
4 Specification
Index of This Section
1 Moving Control Point
2 Changing Degree
3 Changing Number of Division
4 Changing Visual Distance
5 Show/Hide Objects
6 Enable/Disable Hidden Surface/Line Removal
7 Original Shape
8 Rotation of Viewpoint
9 Zoom In/Out
10 Manual/Automatic Animation
11 Benchmark Test
4.1 Moving Control Point (Fig. 1A)
- As shown in Fig. 2, a control point is selected by clicking its neighborhood (2.5 px or less in radius).
When there are 2 or more control points in the radius, the nearest control point is selected. - The selected control point is turned to green (Fig. 2b).
- The control point can be moved by dragging it.
- Only the control points and the lines connecting the control points are shown during the moving (Fig. 2b).
- The destination of the control point is fixed by releasing it.
The world coordinate of the moved control point conserves its z's value before the moving operation, which means that the moving control points are intuitively driven by user. - The Bézier surface is re-drawn with respect to the world coordinate of the moved control point (Fig. 2c).
- The above operation is not allowed in the following cases:
- The control points are not shown.
- During the animation function is activated.
 |
 |
 |
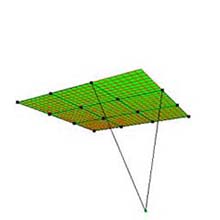
(a) Original shape ("Plane"). |
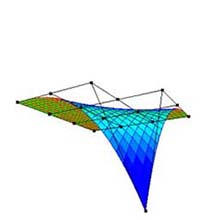
(b) Moving a control point. |
(c) Re-drawing the Bézier surface. |
Fig. 2: Moving a control point (degree: 3×3, subdivision: 25×25). |
||
| Section's Top |
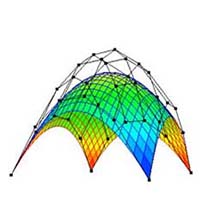
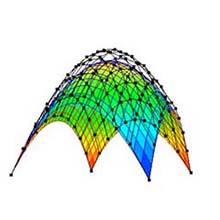
4.2 Changing Degree (Fig. 1a)
- The degree can be changed by dragging the spinner upward/downward (Fig. 3).
- The range of the degree for one dimension is from 1 to 100.
- When the degree is changed, the positions of the control points are reset to their original ones.
- The Bézier surface is re-drawn with respect to the changed degree.
 |
 |
 |
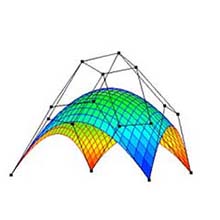
(a) Degree: 3×3. |
(b) Degree: 5×5. |
(c) Degree: 10×10. |
Fig. 3: Changing degree (original shape: "Convex surface", subdivision: 25×25). |
||
| Section's Top |
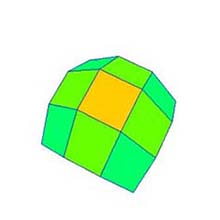
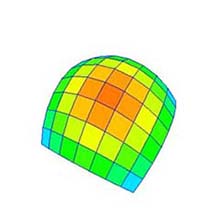
4.3 Changing Number of Division (Fig. 1b)
- The number of division can be changed by dragging the spinner upward/downward (Fig. 4).
- The range of the division for one dimension is from 2 to 300.
- The Bézier surface is re-drawn with respect to the changed number of division.
 |
 |
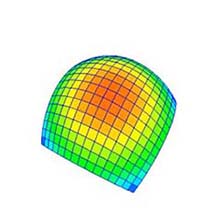 |
(a) Subdivision*: 4×4. |
(b) Subdivision: 8×8. |
(c) Subdivision: 16×16. |
Fig. 4: Changing number of division (original shape: "Convex surface", degree: 25×25). * Let call the number of division as "subdivision" in this document. |
||
| Section's Top |
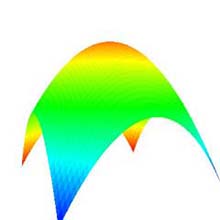
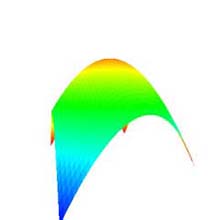
4.4 Changing Visual Distance (Fig. 1c)
- The "angle of field" and the "visual radius" can be changed by dragging the spinner upward/downward (Fig. 5).
- The visual distance is determined by the angle of field and the visual radius, and is not allowed to manipulate directly.
- The types of the angle of field and the visual radius are defined as the integer and the float, respectively.
- The range of the angle of field and the visual radius are from 1 to 180 and from 0.0f to 1000.0f, respectively.
- The Bézier surface is re-drawn with respect to the changed visual distance.
 |
 |
 |
(a) Angle of field: 25°. |
(b) Angle of field: 50 °. |
(c) Angle of field: 100 °. |
Fig. 5: Changing visual distance (original shape: "Convex surface", degree: 10×10, subdivision: 50×50, visual radius: 50.0f). |
||
| Section's Top |
4.5 Show/Hide Objects (Fig. 1d)
4.5.1 Control points and lines connecting them (Control points)
- The control points and the lines connecting them are drawn by checking the check box.
- The control point is black, and is drawn as a square, on a side 5.0f px.
- The line is black, and its width is 1.0f px.
- The control points and the lines connecting them are always visible irrespective of the hidden surface/line removal.
4.5.2 Wire frame (Bezier wires)
- The wire frame is drawn by checking the check box.
- The line width in the wire frame is 1.0f px.
- The
obverse and the
reverse
sides of the wire frame are blue and red, respectively.
The definition of the obverse side is the visible side from the viewpoint at the infinity of the y direction in the world coordinate. - The hidden line removal is applied when the wire frame is shown.
4.5.3 Bézier surface (Bezier surfaces)
- The Bézier surface is drawn by checking the check box.
- The color distribution is determined by the direction of the face, i.e. the obverse side or not.
The obverse and reverse side becomes warm and cold color, respectively, with respect to the y's value in the world coordinate. - The range of the y's value is from -50.0f to 50.0f.
When | y | > 50.0f, they are treated as -50.0f (for y < 0) and 50.0f (for y > 0) only for the color representation. - The hidden surface removal is applied whenever the Bézier surface is shown.
| Section's Top |
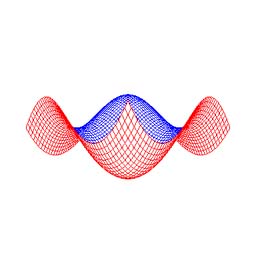
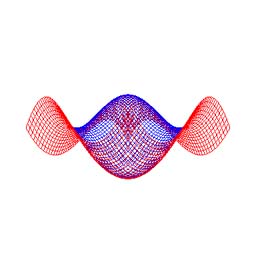
4.6 Enable/Disable Hidden Surface/Line Removal (Fig. 1e)
- The hidden surface/line removal is enabled by checking the check box (Fig. 6).
- The check box is turned to be disabled when the wire frame or the Bézier surface is not shown.
 |
 |
(a) Enabled. |
(b) Disabled. |
Fig. 6: Enable/Disable hidden surface/line removal (original shape: "Sine surface", degree: 10×10, subdivision: 50×50). |
|
| Section's Top |
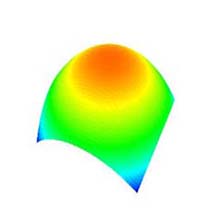
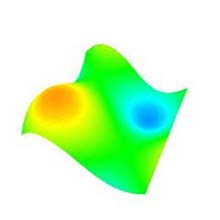
4.7 Original Shape (Fig.1f)
- By selecting the items of the radio button, one of the original shapes, the "Convex surface" (Fig. 7a), the "Sine surface" (Fig. 7b), and the "Plain" (Fig. 7c) is drawn.
- The distance between the 2 control points, which have maximum and minimum value in each coordinate, x, y and z is 100.0f, that is -50.0f~50.0f, except y for the Plain.
 |
 |
 |
(a) Convex surface. |
(b) Sine surface. |
(c) Plain. |
Fig. 7: Original shape (degree: 10×10, subdivision: 50×50). |
||
| Section's Top |
4.8 Rotation of Viewpoint (Fig. 1g)
- The viewpoint is rotated by dragging the translation.
Note that the point of regard is fixed to the origin of the world coordinate. - The azimuth (AZ) θ (theta) and the elevation (EL) φ (phi) are changed by dragging the translation horizontally and vertically, respectively.
- The types of θ and φ are the integers, and are expressed in degree.
| Section's Top |
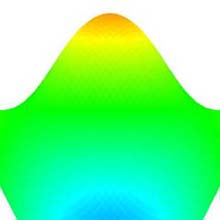
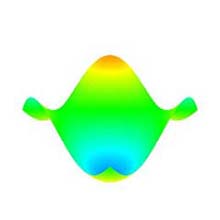
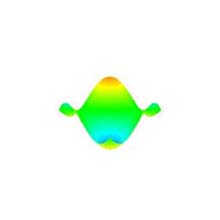
4.9 Zoom In/Out (Fig. 1h)
- The distance between the viewpoint and the point of regard is changed, i.e. zooming in and out, by dragging the translation (Fig. 8).
- The zooming in and out can be done by dragging the translation upward and downward, respectively.
- The type of the distance between the viewpoint and the point of regard is the float.
 |
 |
 |
(a) Zoom in. |
(b) Original shape. |
(c) Zoom out. |
Fig. 8: Zoom in/out (original shape: "Sine surface", degree: 10×10, subdivision: 50×50). |
||
| Section's Top |
4.10 Manual/Automatic Animation (Fig. 1i)
- Animation modes, manual or automatic can be chosen through the radio button.
- During the automatic animation, the rotation and the zooming in/out are turned to be disabled.
- 3 types of the automatic animation, the θ rotation (theta rotation), the φ rotation (phi rotation), and the θ+φ rotation (theta+phi rotation) are provided.
- The benchmark test is turned to be enabled during the automatic animation, and the computational speed is shown.
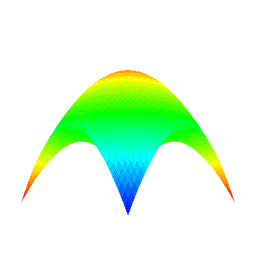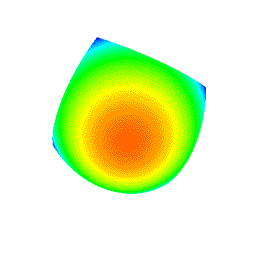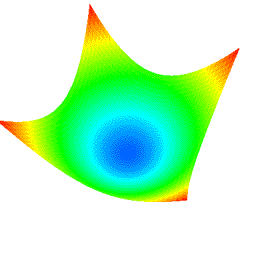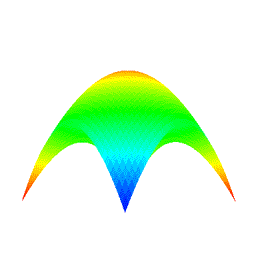 |
Fig. 9: Automatic animation of θ+φ rotation (original shape: "Convex surface", degree: 10×10, subdivision: 50×50)†. † The above animation is deteriorated due to the encoding of GIF format animation. |
| Section's Top |
4.11 Benchmark Test (Fig. 1j)
- The computational speed for the all process, calculating of the deformation of model, the hidden surface/line removal, the perspective projection, and so forth, the rendering (drawing) of the model (shape), and so forth is shown.
- The benchmark test is turn to be disabled, and is initialized to 0.0f, for the following cases:
- When the automatic animation is aborted.
- When the hidden surface/line removal is enabled/disabled.
- The type of the benchmark test result is the float, and is expressed in fps.
| Section's Top | Top |
5 Reported Bug/Disorder
- The window focus is moved to the GLUI from the main window by dragging during the automatic animation.
Reference
- Toby Howard and Ryoichi Mizuno, "Computer Graphics Modeling and Rendering 3: Curves and Surfaces", PPT Lecture at The University of Manchester, A part of , 2002.
| PDF | - Gijyutsu-kei CG Hyojyun Tekisuto-bukku Hensyu-iinkai, "Computer Graphics <Technical CG Standard Textbook>", CG-ARTS Kyokai, 1995 (Heisei 7), (in Japanese
 ).
).
Feedback
Acknowledgment
A part of the English version of this document is supported by Ayako Onzo (Tokyo Institute of Technology
), Bongcheol Park (Korea Advanced Institute of Science and Technology
) and Manabu Ishii (Tokyo Metropolitan Institute of Technology
).
Honor 
- Educational Material at The University of Manchester
 , Instituto Superior de Engenharia de Lisboa
, Instituto Superior de Engenharia de Lisboa , Universität Würzburg
, Universität Würzburg (PDF version), Pontifícia Universidade Católica do Rio Grande do Sul
(PDF version), Pontifícia Universidade Católica do Rio Grande do Sul , and Korea Advanced Institute of Science and Technology (KAIST)
, and Korea Advanced Institute of Science and Technology (KAIST) (PDF version).
(PDF version).
- The German version GUI and instruction have been put on DVD-ROM provided by Arbeitsgemeinschaft Didaktische Innovation GEOMETRIE
 .
.
- Advertisement of BPO
 (PDF version).
(PDF version).
| Top |
Created : 2002/01/29, Modified: 2004/02/18, 2005/03/09 Any distribution/modification of {the source code/this document} without the permission of the copyright owner Copyright © 2002-2005 Ryoichi Mizuno, All Rights Reserved. |
| Top | ![]()
Supplementary Information: Ryoichi Mizuno - Google+ ![]()
![]()