ベジェ曲面
C 言語と OpenGL によるベジェ曲面(線)の描画方法
|
|
目次
1 概要
2 開発環境
3 システムの必要条件
4 仕様
(制御点の移動, 次数の変更, 分割数の変更, 視距離の変更, オブジェクトの表示・非表示, 陰面(線)消去の有効・無効化, 元図形, 視点の回転, ズームイン・アウト, 手動・自動によるアニメーション, ベンチマーク・テスト)
5 既知のバグ・不具合
1 概要
- n×m 次のベジェ曲面を描画する.
- ベジェ曲面の次数、及び分割数は任意に設定することができる.
- 制御点は直感的に移動することができる.
- 透視投影, 及び陰面(線)消去は, 意図的に GPU のようなハードウェアを用いないで実行するように実装されいる.
- Z ソート法のため, 正確に図形を表示できない場合がある.
|
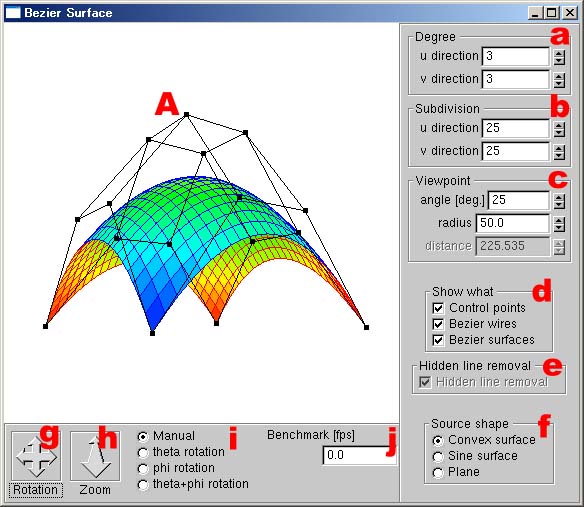
図 1: 本アプリケーションのキャプチャ画像 (Windows XP Professional 上で実行). |
| 先頭へ |
2 開発環境
- C++ (ANSI)
- OpenGL (GLUT for Win32 version 3.7.3, GLUI for Win32 version 2.0 beta)
| 先頭へ |
3 システムの必要条件
3.1 バイナリ
- bs.exe (バイナリ / 188KB)
→ Windows 95 SR2 / 98 / 98 SE / ME / NT4.x / 2000 / XP / 2003 / それ以降
glut32.dll (DLL / 160KB) が必要.
3.2 ソースコード
- HTML 版

→ UNIX (X Window System), Windows 95 / 98 / ME / NT / 2000 / XP / それ以降, OS/2, Mac OS, Be OS など.
X Window System の場合 glx.h をインクルードすることが必要な場合がある.
| 先頭へ |
4 仕様
本節の目次
1 制御点の移動
2 次数の変更
3 分割数の変更
4 視距離の変更
5 オブジェクトの表示・非表示
6 陰面(線)消去の有効・無効化
7 元図形
8 視点の回転
9 ズームイン・アウト
10 手動・自動によるアニメーション
11 ベンチマーク・テスト
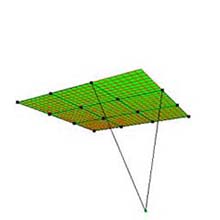
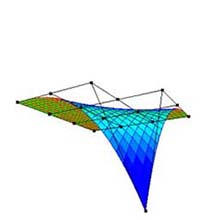
4.1 制御点の移動 (図 1A)
- 図 2 に示すように, 制御点の近傍 (半径 2.5 px 以内) をクリックすることにより選択する.
その近傍に 2 つ以上の制御点がある場合, 最近傍の制御点が選択される. - 選択された制御点は緑色になる (図 2b).
- ドラッグすることで, 制御点を移動できる.
- 移動中は, 制御点とそれを連結する線分のみが表示される (図 2b).
- リリースすることで, 制御点の移動後の位置が決定される.
ユーザが直感的に制御点を移動できるように, 移動した制御点のワールド座標は, 移動前の奥行値を保存する. - 移動後の制御点に対応したベジェ曲面が再描画される (図 2c).
- 上記の操作は以下の場合行いえない:
- 制御点が表示されていない場合.
- アニメーション機能がアクティブな場合.
 |
 |
 |
(a) 元図形 ("平面"). |
(b) 制御点の移動. |
(c) ベジェ曲面の再描画. |
図 2: 制御点の移動 (次数: 3×3, 分割数: 25×25). |
||
| 節の先頭へ |
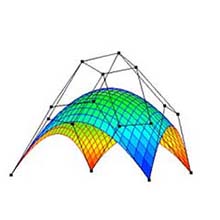
4.2 次数の変更 (図 1a, GUI においては, "Degree")
- スピナー (図 1a) を上下にドッラグすることにより次数を変更することができる (図 3).
- 各軸の次数は 1 から 100 までの範囲である.
- 次数を変更すると, 制御点の位置は元図形に戻る.
- ベジェ曲面は次数の変更に応じて再描画される.
 |
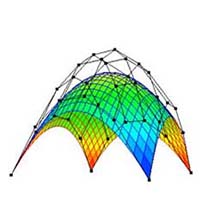 |
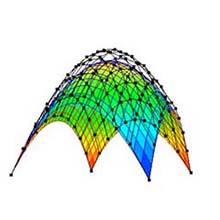 |
(a) 次数: 3×3. |
(b) 次数: 5×5. |
(c) 次数: 10×10. |
図 3: 次数の変更 (元図形: "凸曲面", 分割数: 25×25). |
||
| 節の先頭へ |
4.3 分割数の変更 (図 1b, GUI においては, "Subdivision")
- スピナー (図 1b) を上下にドッラグすることにより分割数を変更することができる (図 4).
- 各軸の分割数は 2 から 300 までの範囲である.
- ベジェ曲面は分割数の変更に応じて再描画される.
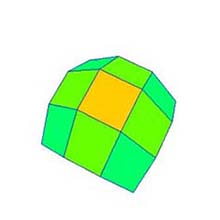 |
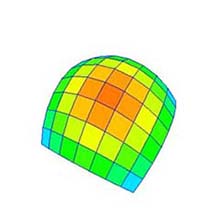 |
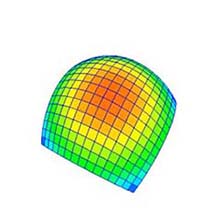 |
(a) 分割数*: 4×4. |
(b) 分割数: 8×8. |
(c) 分割数: 16×16. |
図 4: 分割数の変更 (元図形: "凸曲面", 次数: 25×25). * GUI においては, 分割(数)"Division" ではなく "Subdivision" と表記するものとする. |
||
| 節の先頭へ |
4.4 視距離の変更 (図 1c, GUI においては, "View point")
- "angle" (画角) と "radius" (視半径) スピナー (図 1c) を上下にドッラグすることにより視距離を変更することができる (図 5).
- 視距離 (visual distance) は画角と視半径によって決定され, 直接変更することはできない.
- 画角, 及び視半径は, それぞれ整数 (int 型), 浮動小数 (float 型) として定義される.
- 画角, 及び視半径は, それぞれ 1 から 180 まで, 0.0f から 1000.0f までの範囲である.
- ベジェ曲面は視距離の変更に応じて再描画される.
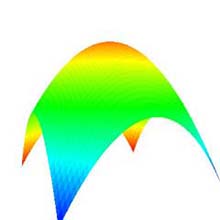 |
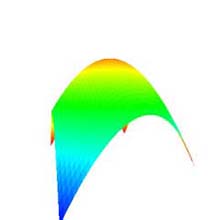 |
 |
(a) 画角: 25°. |
(b) 画角: 50 °. |
(c) 画角: 100 °. |
図 5: 視距離の変更 (元図形: "凸曲面", 次数: 10×10, 分割数: 50×50, 視半径: 50.0f). |
||
| 節の先頭へ |
4.5 オブジェクトの表示・非表示 (図 1d, GUI においては, "Show what")
4.5.1 制御点, 及びそれらを連結する線分 (GUI においては, "Control points")
- 制御点, 及びそれらを連結する線分はチェックボックスにチェックを入れることにより描画される.
- 制御点は黒色の一辺が 5.0f px の正方形で描画される.
- 制御点を連結する線分は黒色の幅 1.0f px の線分で描画される.
- 制御点, 及びそれらを連結する線分は陰面(線)消去の有無にかかわらず表示される.
4.5.2 ワイヤーフレーム (GUI においては, "Bezier wires")
- ワイヤーフレームはチェックボックスにチェックを入れることにより描画される.
- ワイヤーフレーム幅 1.0f px の線分で描画される.
- 表面, 及び裏面は, それぞれ青色, 赤色で描画される.
表面はワールド座標の y 軸無限遠から可視である面と定義する. - 陰線消去はワイヤーフレームが表示されている場合のみ適用できる.
4.5.3 ベジェ曲面 (GUI においては, "Bezier surfaces")
- ベジェ曲面はチェックボックスにチェックを入れることにより描画される.
- 色分布は面の方向(表面か裏面か)によって決定される.
表面, 及び裏面は, それぞれワールド座標の y の値に応じた暖色, 寒色で表現される. - この y の値は -50.0f から 50.0f までの範囲である.
| y | > 50.0f の場合, 色の表現についてのみ -50.0f (y < 0 の場合), 及び 50.0f (y > 0 の場合) とする. - 陰面消去はベジェ曲面が表示されている場合のみ適用できる.
| 節の先頭へ |
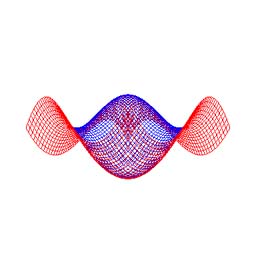
4.6 陰面(線)消去の有効・無効化 (図 1e, GUI においては, "Hidden line removal")
- 陰面(線)消去はチェックボックスにチェックを入れることにより有効になる (図 6).
- チェックボックスはワイヤーフレーム, 及びベジェ曲面のどちらも表示されていない場合, 無効化される.
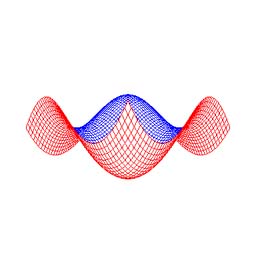 |
 |
(a) 有効. |
(b) 無効. |
図 6: 陰面(線)消去の有効・無効化 (元図形: "正弦波曲面", 次数: 10×10, 分割数: 50×50). |
|
| 節の先頭へ |
4.7 元図形 (図 1f, GUI においては, "Source shape")
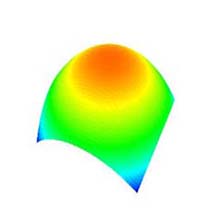
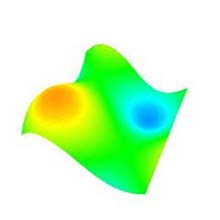
- ラジオボタンの項目を選択することにより, 元図形 "凸曲面 (Convex surface)" (図 7a), "正弦波曲面 (Sine surface)" (図 7b), "平面 (Plain)" (図 7c) が描画される.
- 元図形の制御点の x, y, z 各座標の最小値, 及び最大値は, それぞれ -50.0f, 50.0f である. 但し, 平面の y 座標を除く.
 |
 |
 |
(a) 凸曲面 (Convex surface). |
(b) 正弦波曲面 (Sine surface). |
(c) 平面 (Plain). |
図 7: 元図形 (次数: 10×10, 分割数: 50×50). |
||
| 節の先頭へ |
4.8 視点の回転 (図 1g, GUI においては, "Rotation")
- 視点はトランスレーションをドラッグすることにより回転することができる.
但し, 注視点はワールド座標の原点に固定されている. - 方位角 (AZ) θ (シータ), 及び仰角 (EL) φ (ファイ) は, それぞれトランスレーションを横, 縦にトランスレーションをドラッグすることにより変化させることができる.
- θ, φ は整数 (int 型) 360° 法で表現される.
| 節の先頭へ |
4.9 ズームイン・アウト (図 1h, GUI においては, "Zoom")
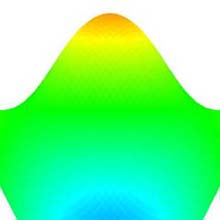
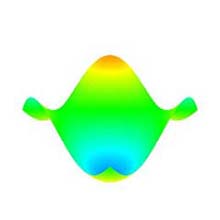
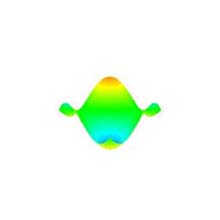
- 視点と注視点間の距離はトランスレーションをドラッグすることにより変化させる(ズームイン・アウト)ことができる (図 8).
- ズームイン, 及びズームアウトは, それぞれトランスレーションを上, 下にドラッグすることによって可能となる.
- 視点と中止転換の距離は浮動小数 (float 型) で表現される.
 |
 |
 |
(a) ズームイン. |
(b) 元図形. |
(c) ズームアウト. |
図 8: ズームイン・アウト (元図形: "正弦波曲面", 次数: 10×10, 分割数: 50×50). |
||
| 節の先頭へ |
4.10 手動・自動によるアニメーション (図 1i)
- ラジオボタンを選択することにより, 手動 (Manual) 及び自動によるアニメーションのモードを選択することができる.
- 自動によるアニメーション中は, 視点の回転とズームイン・アウトは無効化される.
- θ 回転 (theta rotation), φ 回転 (phi rotation), θ+φ 回転 (theta+phi rotation) の 3 種の自動によるアニメーションが提示されている.
- 計算速度を表示するベンチマーク・テスト (Benchmark) は自動によるアニメーション中に有効になる.
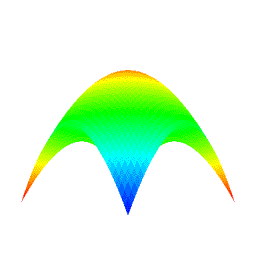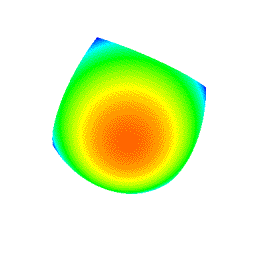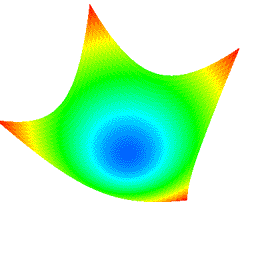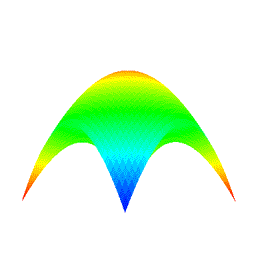 |
図 9: θ+φ 回転の自動によるアニメーション (元図形: "凸曲面", 次数: 10×10, 分割数: 50×50)†. † 上のアニメーションは GIF フォーマットアニメーションであるため劣化している. |
| 節の先頭へ |
4.11 ベンチマーク・テスト (図 1j, GUI においては, "Benchmark")
- 図形の変形・陰面(線)消去・透視投影など, 及び図形のレンダリング(描画)などのすべてのプロセスにかかる計算速度が表示される.
- ベンチマーク・テストは下記の場合, 無効化され, 0.0f に初期化される:
- 自動によるアニメーションが中止された場合.
- 陰面(線)消去が有効化, または無効化された場合.
- ベンチマーク・テストの結果は浮動小数 (float 型) で表現され, 単位は fps である.
5 既知のバグ・不具合
- 自動によるアニメーション中, ウィンドウのフォーカスがメイン・ウィンドウから GLUI に移動する.
参考文献
- Toby Howard and Ryoichi Mizuno, "Computer Graphics Modeling and Rendering 3: Curves and Surfaces", マンチェスター大学講義用 PPT, 一部引用, 2002.
| PDF | - 技術系 CG 標準テキストブック編集委員会, "コンピュータグラフィックス: 技術系 CG 標準テキストブック", CG-ARTS 協会, 1995 (平成 7), (日本語
 ).
).
フィードバック
謝辞
本稿の英語版の一部は Ayako Onzo (東京工業大学
), Bongcheol Park (Korea Advanced Institute of Science and Technology
), Manabu Ishii (首都東京大学
) の協力を得て作成された.
オナー 
- マンチェスター大学
 , Instituto Superior de Engenharia de Lisboa
, Instituto Superior de Engenharia de Lisboa , ヴュルツブルク大学
, ヴュルツブルク大学 (PDF 版), Pontifícia Universidade Católica do Rio Grande do Sul
(PDF 版), Pontifícia Universidade Católica do Rio Grande do Sul , Korea Advanced Institute of Science and Technology (KAIST)
, Korea Advanced Institute of Science and Technology (KAIST) (PDF 版) の教材として採用.
(PDF 版) の教材として採用.
- ドイツ語版の GUI の本バイナリが Arbeitsgemeinschaft Didaktische Innovation GEOMETRIE
 が発行した DVD-ROM に収録.
が発行した DVD-ROM に収録.
- BPO
 (PDF 版) の広告として採用.
(PDF 版) の広告として採用.
| 先頭へ |
作成 : 2002/01/29, 改訂: 2004/02/18, 2005/03/09 著作者に無断でソースコードや本稿を頒布・改変することを禁じます. Copyright © 2002-2015 Ryoichi Mizuno, All Rights Reserved. |
| 先頭へ | ![]()
補足情報: Ryoichi Mizuno - Google+ ![]()
![]()