Programs:

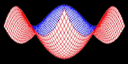
• OpenGL: Bézier Surface [Open-source]
  A Bézier Surface is a parametric tensor product surface defined by mathematical formulae, used in computer graphics, computer-aided design, and finite element modeling. It can be viewed as a generalization of a Bézier curve.
    Educational Material at The University of Manchester, Instituto Superior de Engenharia de Lisboa,
         Universität WEzburg (PDF version), Pontifícia Universidade Católica do Rio Grande do Sul, and
         Korea Advanced Institute of Science and Technology (KAIST) (PDF version).
    The German version GUI and instruction have been put on DVD-ROM provided by
         Arbeitsgemeinschaft Didaktische Innovation GEOMETRIE.
    Advertisement of BPO (PDF version).
    Featured by Masdel Blog (PDF version).
    Cited by Wikipedia: Bézier surface (en version).
  
  — The alternative version written in Japanese is also available.
  

• OpenGL: Tour Into the Picture [Open-source]
  Tour Into the Picture (TIP) is for easily making animations from one 2D picture or photograph of a scene.
    Educational Material at ETH Zürich (PDF version), University of Illinois at Urbana (PDF version), and Sejong University (PDF version).
  
  — The alternative version written in Japanese is also available.
   
• Java Applet: Mandelbrot Set [Open-source]
  The Mandelbrot Set has become popular far outside of mathematics both for its aesthetic appeal and its complicated structure, arising from a simple definition. This is largely due to the efforts of Benoit Mandelbrot (and others), who worked hard to communicate this area of mathematics to the general public.
    An image generated by this applet has been used in
        The Humble Approach Initiative symposium program book on Mathematics and Its Significance (PDF/web version).
   
• Java Applet: The Game of Life [Open-source]
  The Game of Life is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is the best-known example of a cellular automaton.
    Educational Material at der Ludwigs-Maximilians-Universität München (PDF version).
   
• Java Applet: Branching: L-system Tree [Open-source]
  An L-system or Lindenmayer system is a formal grammar (a set of rules and symbols) most famously used to model the growth processes of plant development, though able to model the morphology of a variety of organisms.
   Used in Bio-Inspired Artificial Intelligence published by The MIT Press
       (webpages of {Exact page/The MIT Press} and PDF versions of {Front page/Exact page/The MIT Press}).
   Cited by A. Nordin et. al. "Generative Design Systems for the Industrial Design of Functional Mass Producible Natural-Mathematical Forms" published by IASDR (PDF version).
    Cited by Wikipedia: L-system (en/jp version) and Simulated growth of plants (en version).
   
• Java Applet: Bifurcation of Logistic Map [Open-source]
  The Logistic Map is a polynomial mapping, often cited as an archetypal example of how complex, chaotic behavior can arise from very simple non-linear dynamical equations.
    Educational Material at The University of Tokyo.
   
• C: The Lorentz Attractor [Open-source]
  The Lorenz Attractor, introduced by Edward Lorenz in 1963, is a non-linear three-dimensional deterministic dynamical system derived from the simplified equations of convection rolls arising in the dynamical equations of the atmosphere.
    An image generated by this program has been used in Fluid Mechanics and the SPH Method: Theory and Application published by Oxford University Press (PDF/image/full text version).
    An image generated by this program has been used in Double Bubble Universe (PDF/image/web/paper media version).
    Featured by Google Code (PDF version 1 2), Grasshopper (PDF version), and Serving History (PDF version).
    Cited by Wikipedia: Lorenz attractor (en/jp version).
  
  — The alternative version written in Japanese is also available.
  

[ Page Top ]
Supplementary Information: Ryoichi Mizuno - Google+